INTERPOLATION
The final step in the process is to interpolate between each of the surrounding values. This is sort of ‘averaging out’ the surrounding values. However, it is not as simple as just finding the mean of the values. Interpolation is finding a value in between two numbers, but it can be weighted to either side.
In our case we want to weight the values based on how close the candidate point is to the grid vertex. In our 2D example, we have 4 points, which we need to interpolate both in the x and y direction.
Interpolated Value = A + (weight * (B - A))
INTERPOLATION DEMO
Linear Interpolated Value:
Smoothstep Interpolated Value:
Smootherstep Interpolated Value:
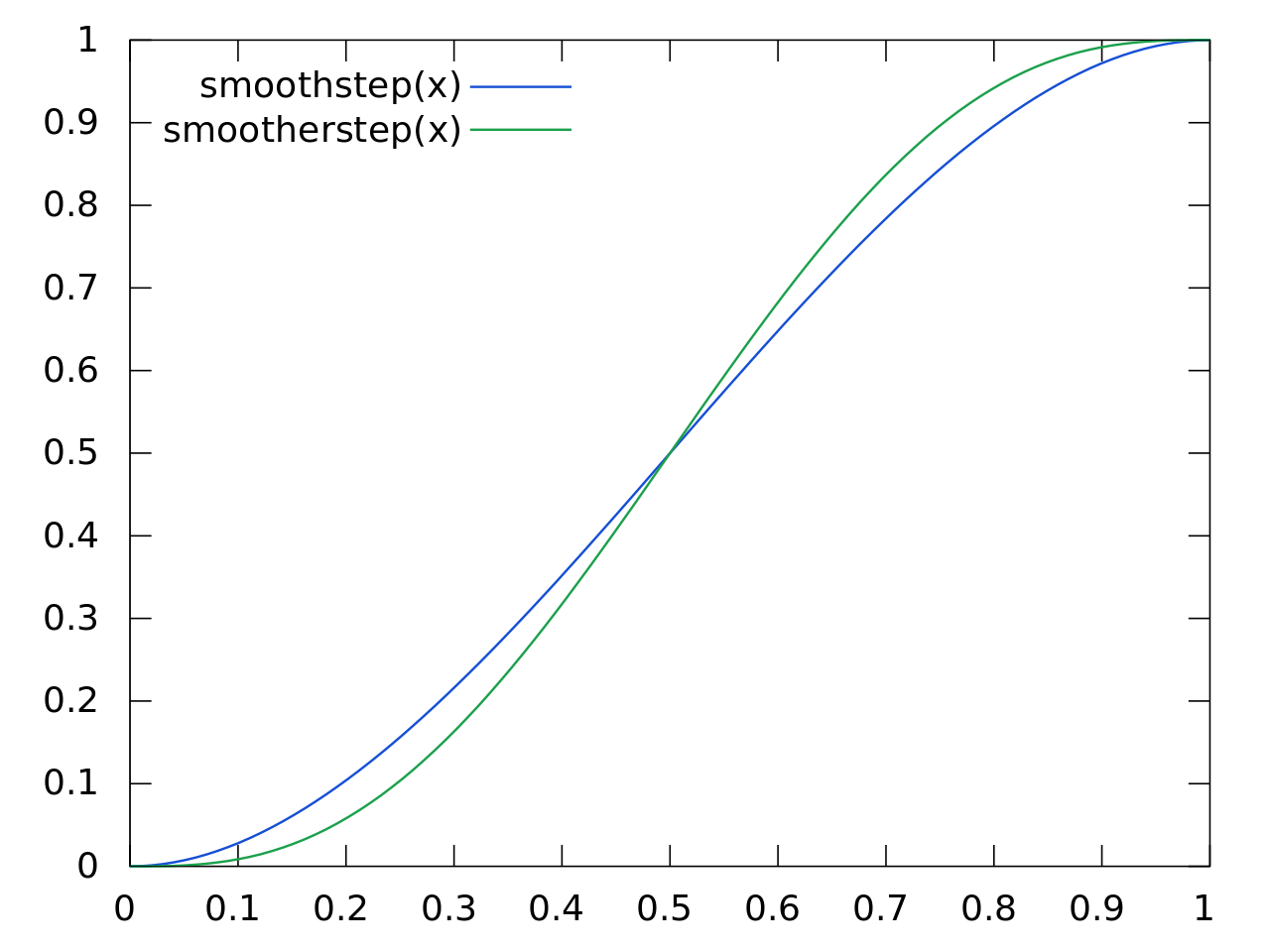
Most interpolation with perlin noise often doesn’t use what we call a ‘linear’ interpolation’ as shown above. More often than not, we use a smoother interpolation function such as 'Smoothstep' or 'Smoothersep'.
These smoothing functions just modify the weight slightly so we get a smoother gradient between the evaluated points.
Finally, we should have one single value for our candidate point. This is a floating point value, and represents the value of the noise at this position in space.